Tags: Week 1 : Introduction to Machine Learning

C1_W1_Lab03_Cost_function_Soln.ipynb

---

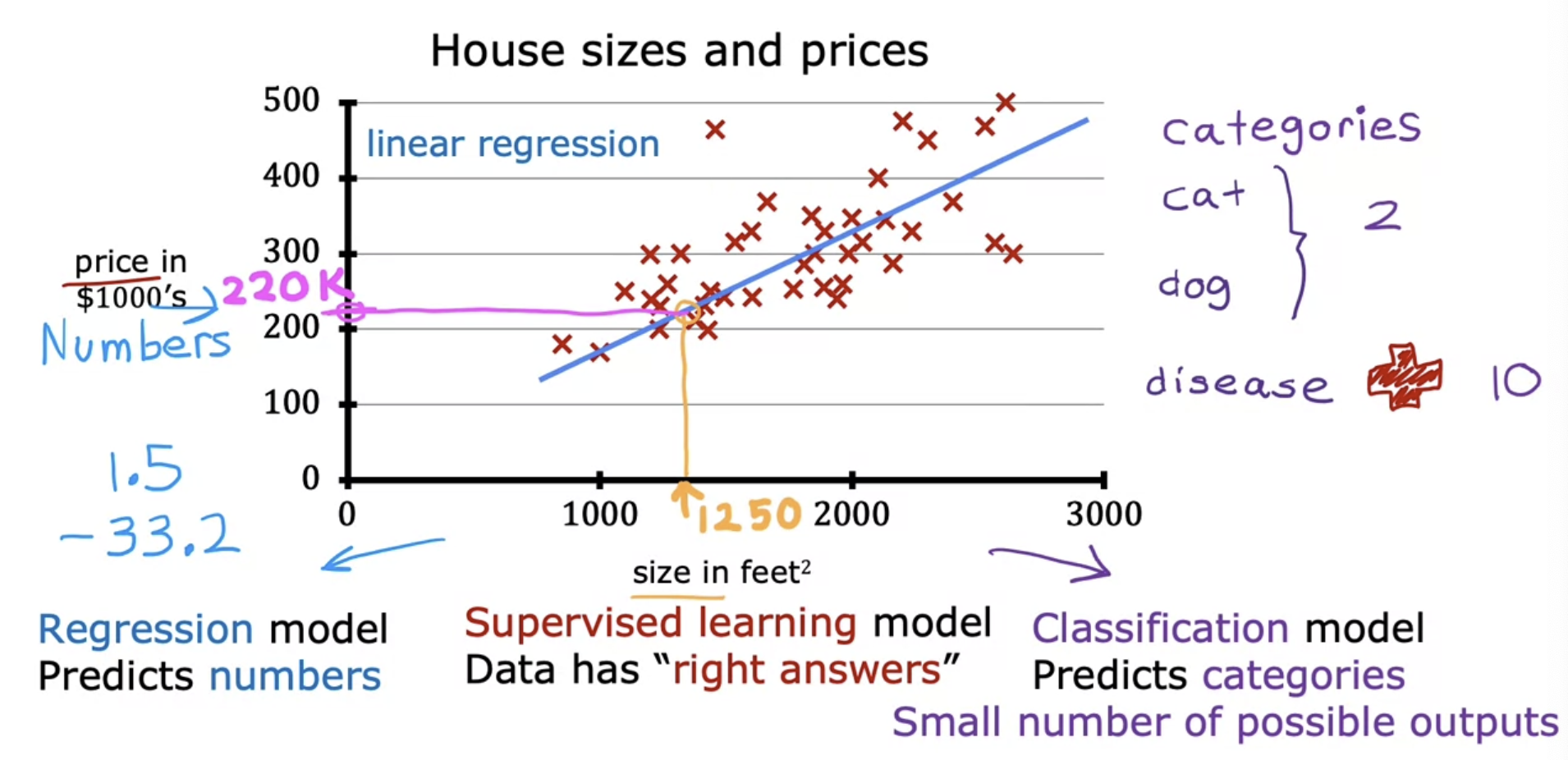
Regression 정의

Regression is to predict numbers

Any supervised learning model that predicts a number such as 220,000 or 1.5 or negative 33.2 is addressing what’s called a regression problem

Linear Regression

• Fitting a straight line to your dataset
• Regression인데 선형인 regression, not 비선형
• Linear regression builds a model which establishes a relationship between features and targets
• The model has two parameters $w$ and $b$ whose values are ‘fitted’ using training data.
• Supervised Learning

• Also called “one variable(a single feature)” or “Univariate(one variable) Linear Regression”

  

(Predictive) Function

\[f_{w,b}​(x)=wx+b\]

• $f$ : Hypothesis(Historically, This function used to called as)
• $\hat{y}$ : Estimated or predicted value of $y$
• $y$ : Target(or Label), which is actual true value in the training set
• $x$ : Input or input feature
• $w$ : parameter: weight
• $b$ : parameter: bias
• Subscript $w$, $b$ of $f_{w,b}(x)$ : $w$, $b$ are fixed, which are **always a constant value

Parameters

• $w$ and $b$ will determine the prediction $\hat{y}$ based on the input features $x$. The function takes $x$ as input, and depending on the values of $w$ and $b$, $f$ will output a prediction $\hat{y}$
• In machine learning, parameters of the model are the variables you can adjust during training in order to improve the model
• Parameters also are referred to as coefficients or weights

Cost Function

머신러닝 모델은 예측값과 실제값의 차이가 최소화되는 방향으로 parameters($w$, $b$)을 수정(Update)함

\[\min_{w,b} \ J(w, b)\]

• 손실함수 $J(w, b)$를 최소화하는 $w$, $b$(min 하첨자)를 찾는 수학적 표현

Function

Note: There are many different type of cost functions, except below cost function

\[J(w,b) = \frac{1}{2m}∑^m_{i=1}(f_{w,b}(x^{(i)})−y^{(i)})^2\]

• $m$ : number of training examples
• $f_{w,b}(x^{(i)})$ = $\hat{y}^{(i)}$ : Prediction value
• $y^{(i)}$ : Target
• Error : $f_{w,b}(x^{(i)})-y^{(i)}$
• $m$ : number of training examples
• By convention, the cost function that machine learning people use actually divides by 2 times m. The extra division by 2 is just meant to make some of our later calculations look neater, but the cost function still works whether you include this division by 2 or not
• Called as Squared Error Cost Function

Intuition

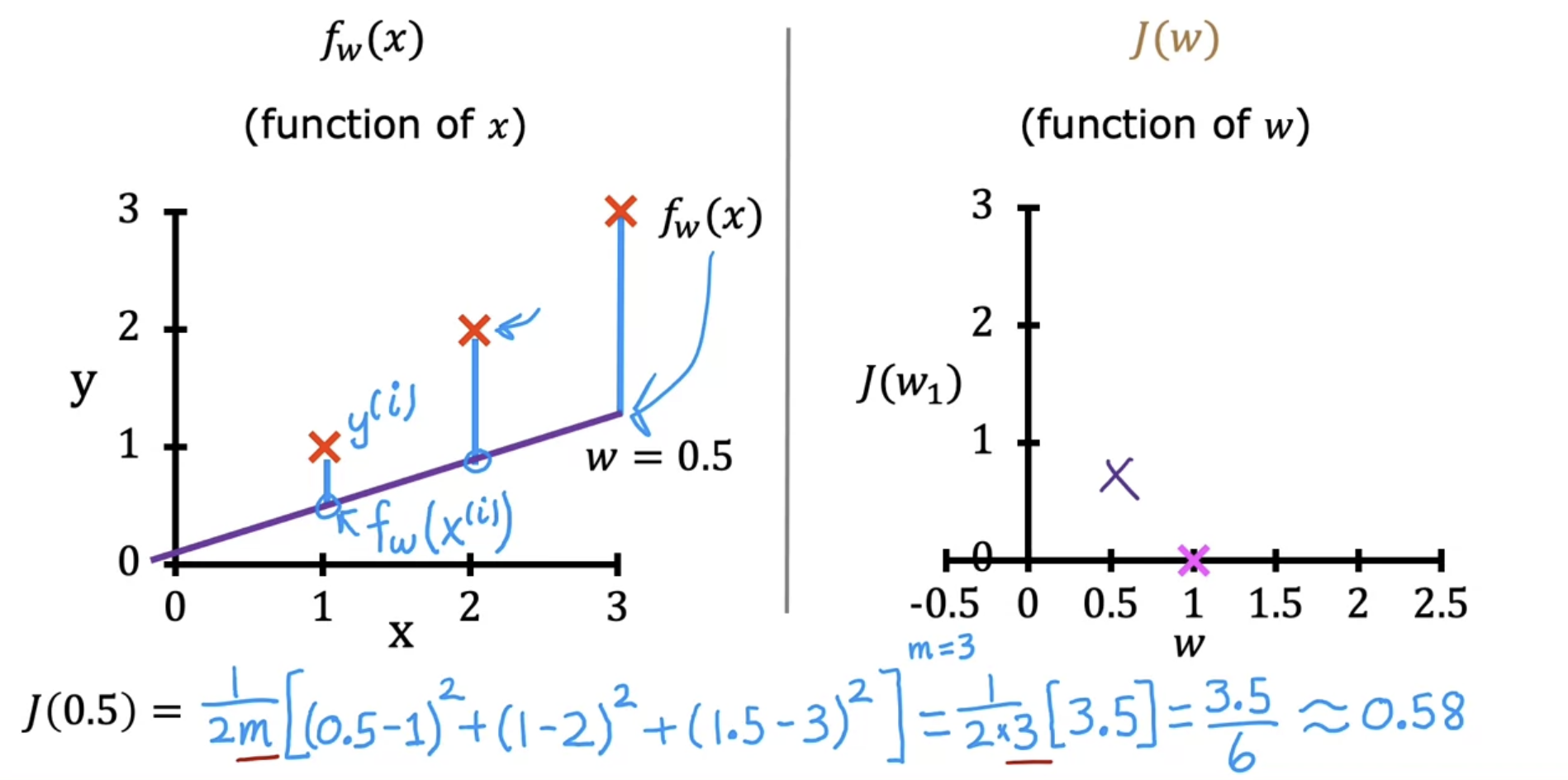
Predictive linear function is a function of the input $x$

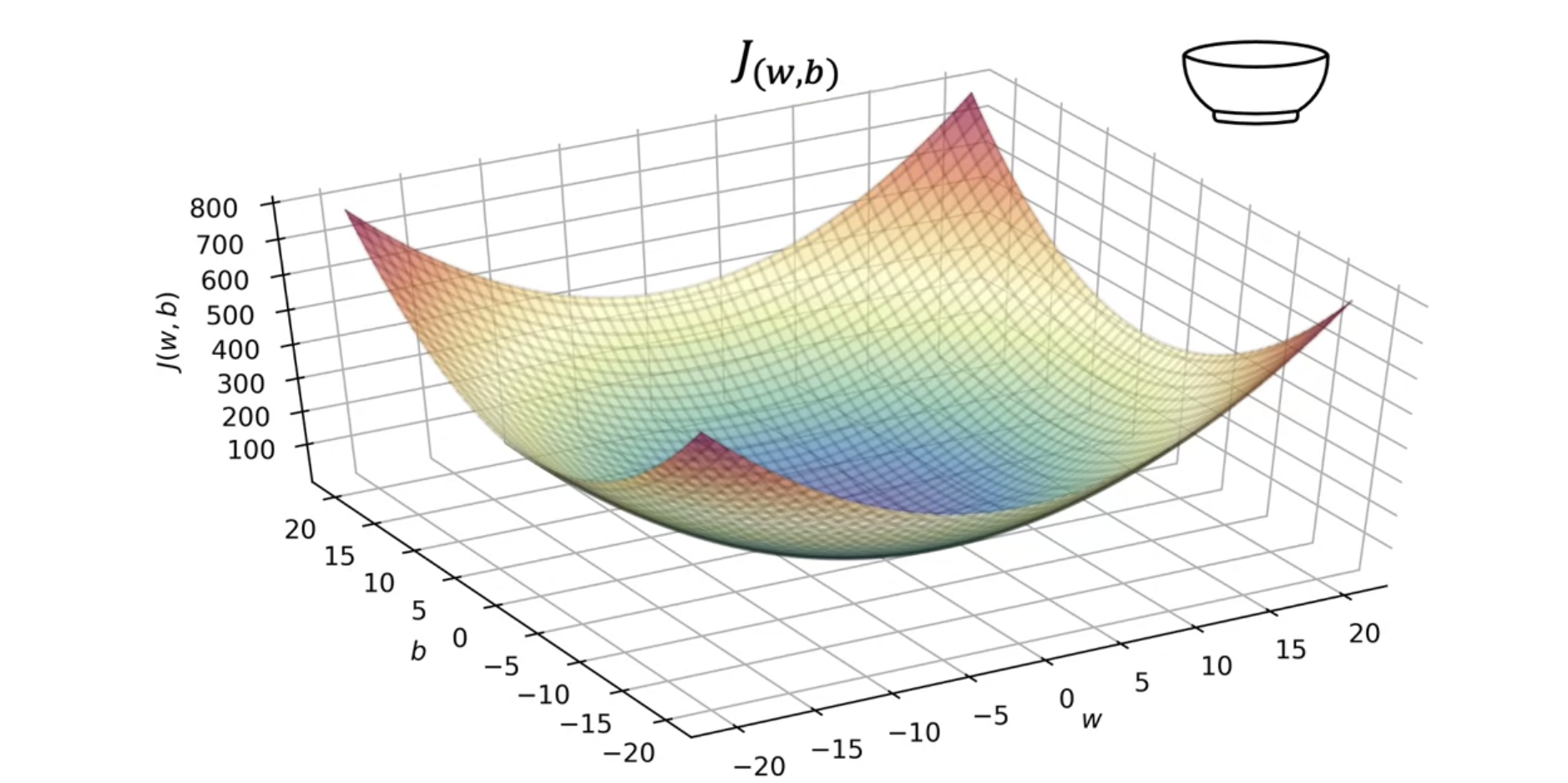
Cost function is a function of the parameter w, the horizontal axis is now labeled w and not x of function, and the vertical axis is now J and not y of function

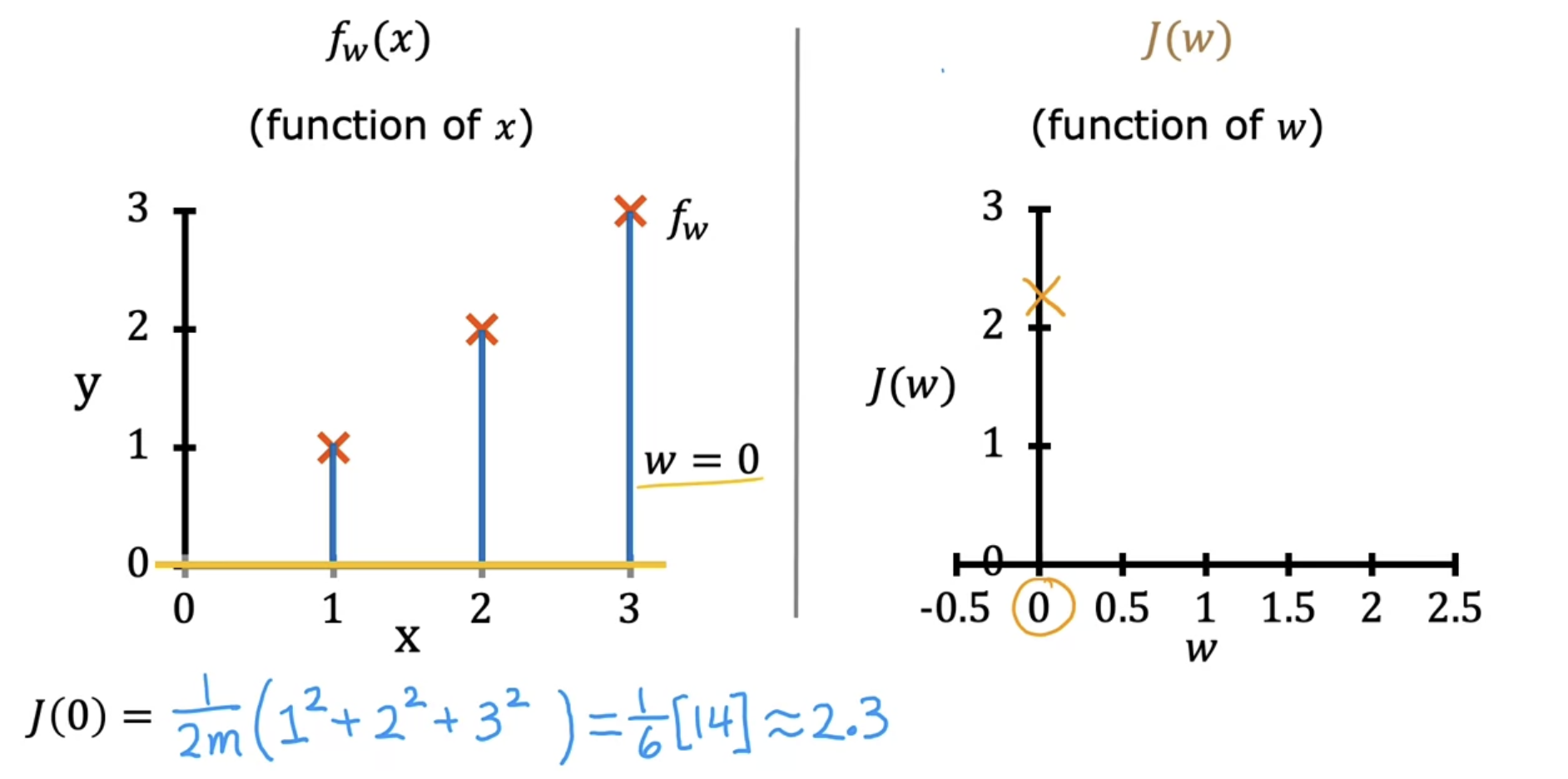
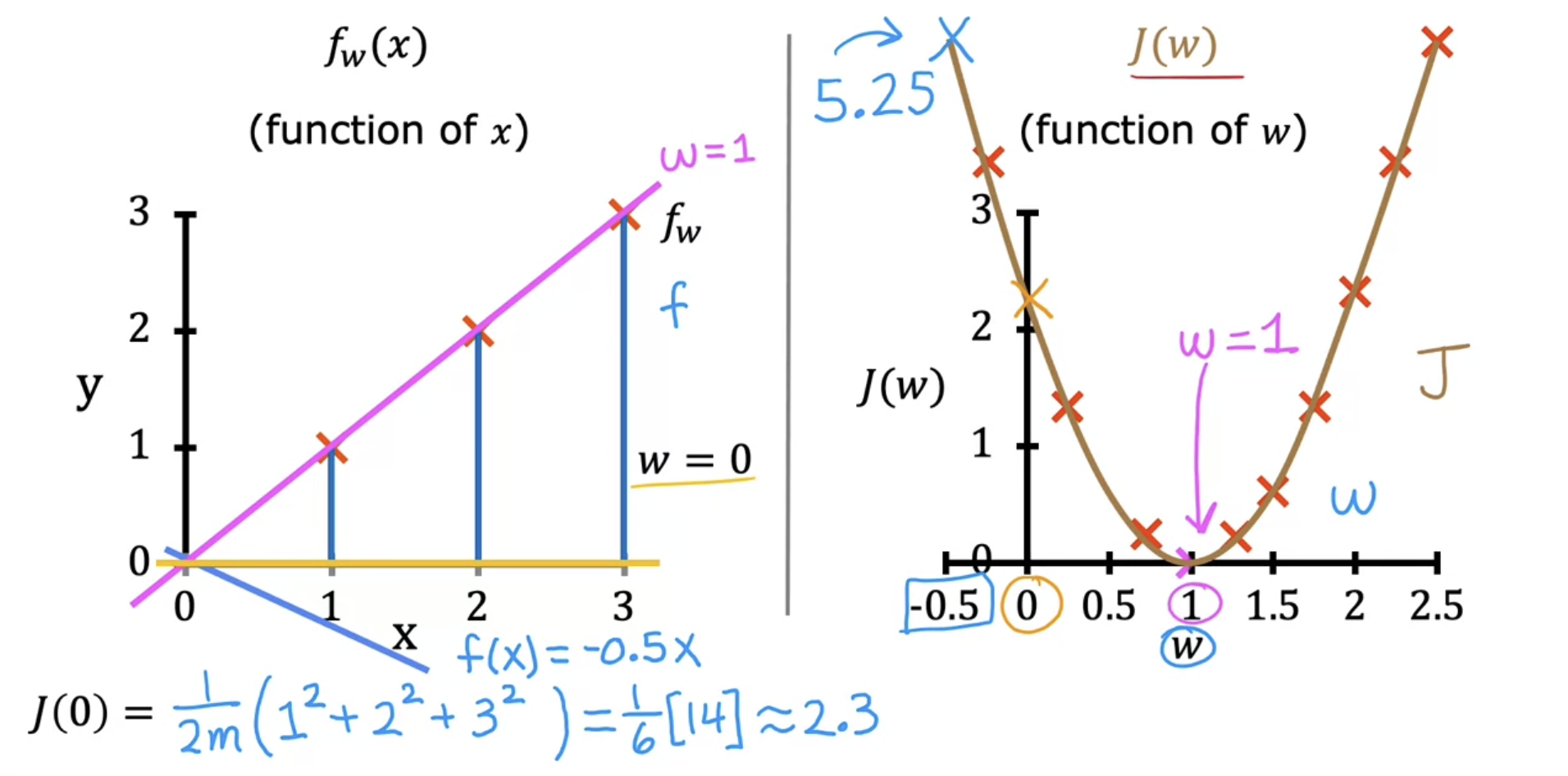
(1) With parameter $w$ only, being $b = 0$

• Model : $f_{w}(x)=wx$
• Parameters : $w$
• Cost function : $J(w) = \frac{1}{2m}∑^m_{i=1}(f_{w}(x^{(i)})−y^{(i)})^2$
• Goal : $\min_{w} \ J(w)$

• 그래프로 쉽게 이해하기

  

  

  

(2) With parameter $w$, $b$

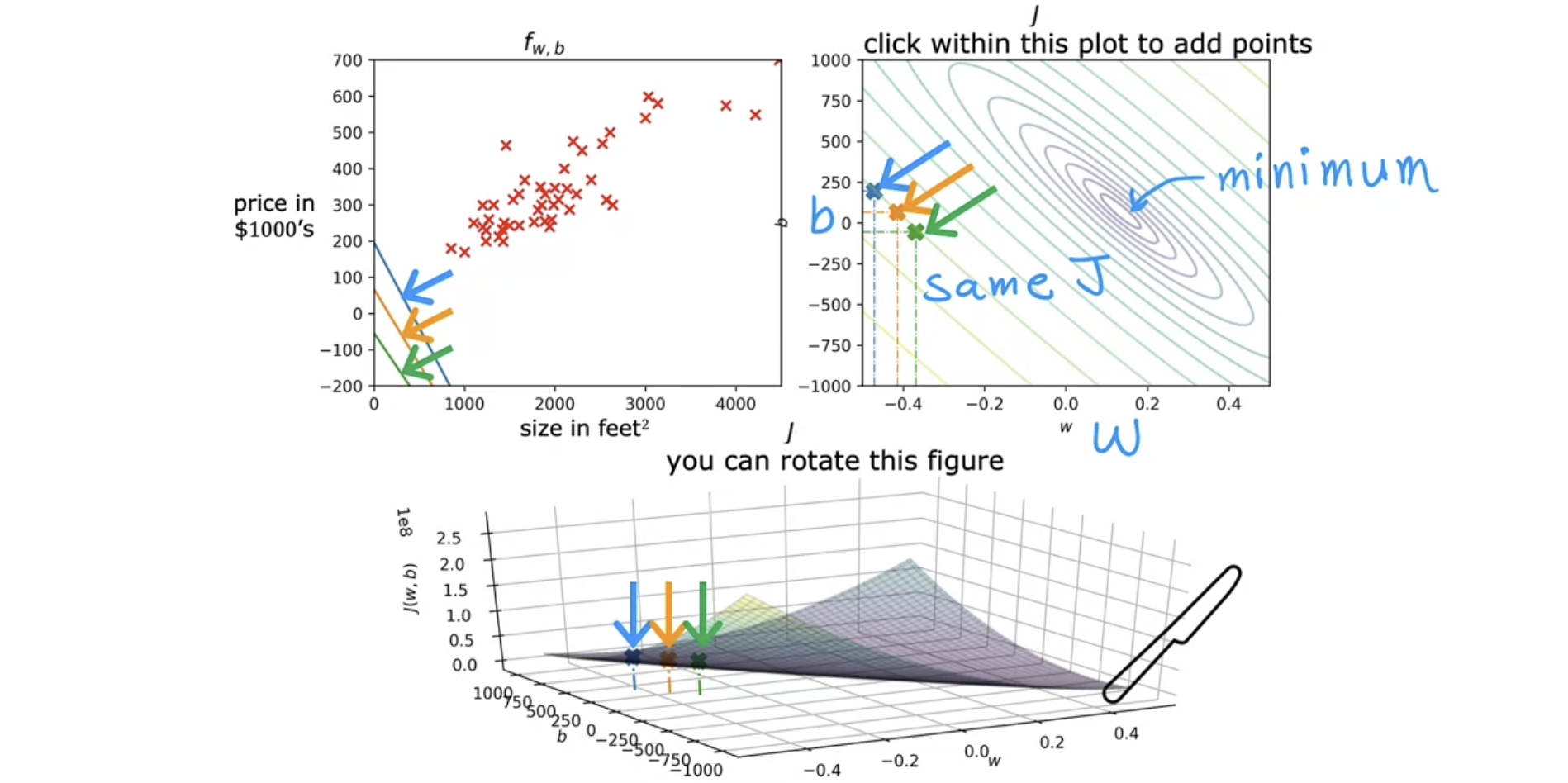
• Model : $f_{w,b}(x)=wx+b$
• Parameters : $w, b$
• Cost function : $J(w,b) = \frac{1}{2m}∑^m_{i=1}(f_{w,b}(x^{(i)})−y^{(i)})^2$
• Goal : $\min_{w, b} \ J(w, b)$

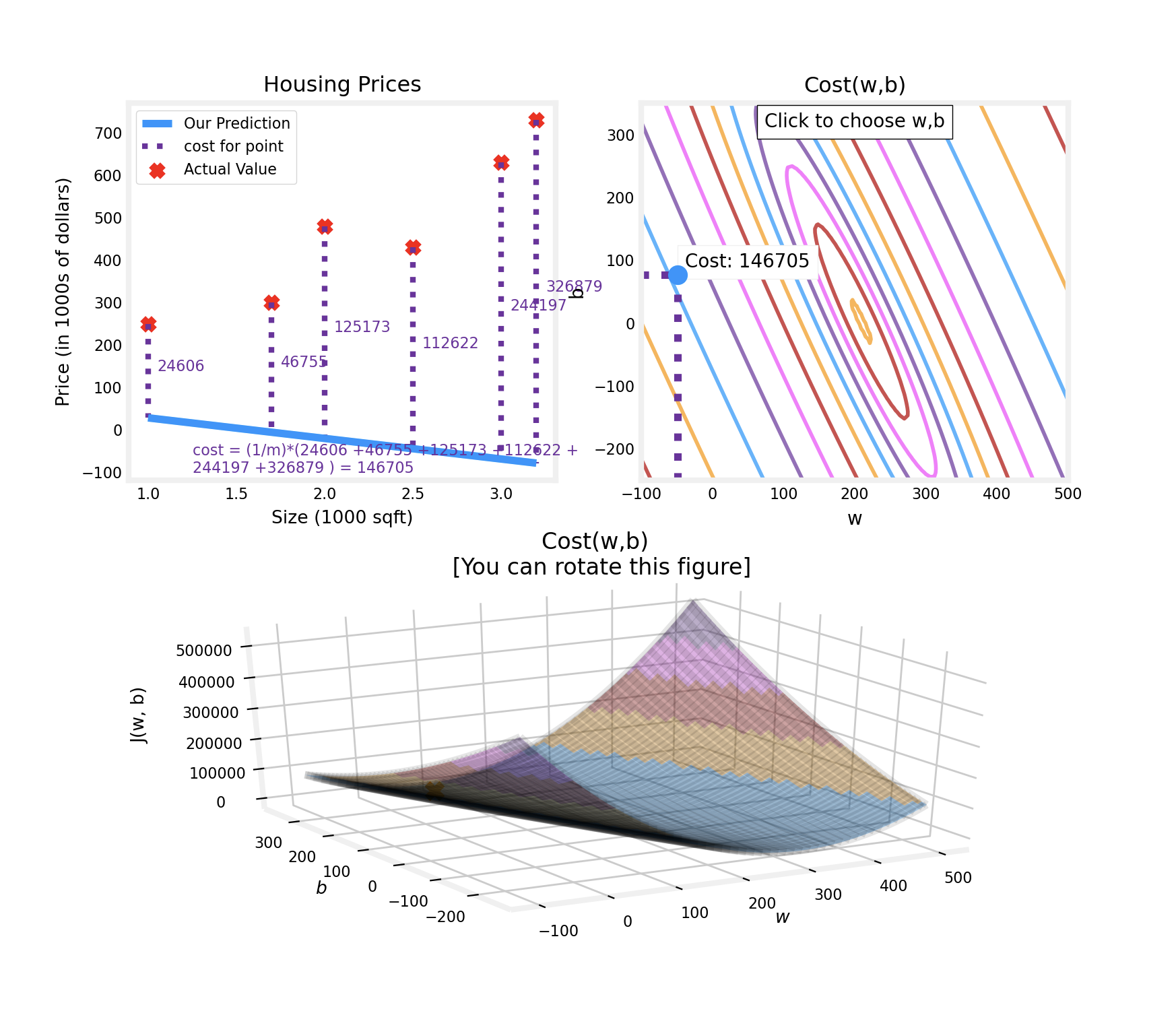
• Examples1 : 손실함수값이 minimum에서 멀리있다

  

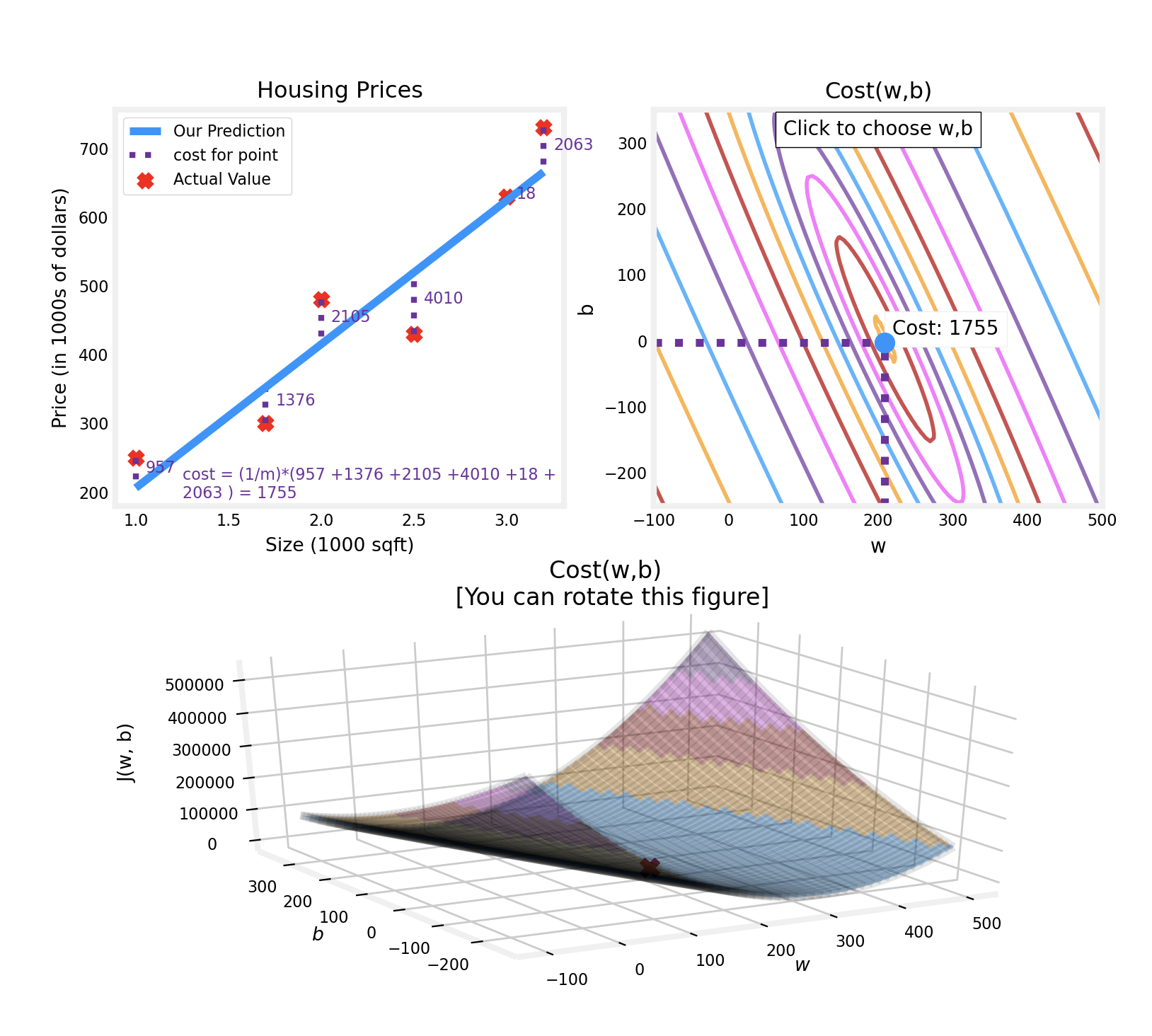
• Examples2 : 손실함수값이 minimum에 있음