용어
표본공간(Sample Space)
모집단에 대하여 모든 개체의 속성을 조사하기 전에는 어떤 결과가 나온다고 확실히 말할 수 없다. 그러나 속성의 가능한 모든 결과를 나열하거나 표현하는 것은 가능하다. 이때 가능한 속성의 모든 결과를 표본공간(집합) 또는 간단히 공간이라 하고 $S$, $\Omega$ 등으로 나타낸다.
표본공간은 사건공간이라고도 함
사건(Event)
\[사건 \subset 표본공간\]표본공간이 $S$인 확률 실험에서 사건이란 그 사건이 일어날 확률을 정의할 수 있는 $S$(표본공간)의 부분집합을 말한다. 표본공간 $S$가 유한하거나 가산이면 모든 부분집합이 사건이 된다. 실험 결과(Outcome)가 어떤 사건(Event)의 원소이면 그 사건이 일어났다고 한다.
(1) **사건의 표현**
사건은 알파벳 대문자 $A, B, C, \dots$ 를 이용하여 나타내는 것이 일반적이다. 사건은 원소를 모두 나열하여 나타내기도 하고(원소나열법, 사건이 일어나는 조건을 이용하여 나타내기도 한다(조건제시법)
예를 들어 앞면(H)과 뒷면(T)을 갖는 동전을 두 번 던지는 실험을 한다면 표본공간은
\[S = \{HH, HT, TH, TT\}\]이다. $A$를 앞면이 적어도 한 번 나오는 사건이라고 하면 다음과 같이 표현할 수 있다
\[A={\text{앞면이 적어도 한 번 나온 결과}} = \{HH, TH, HT\}\](2) $P(A)$ 읽는 방법
\[P(A) : \text{A라는 사건이 일어날 확률}\]또는 정확하게 표현하면
\[P(A) = Probability(\text{Outcome} \isin A)\]→ 특정 결과(Outcome)가 사건 A 집합에 속할 확률
조건부확률
일반적으로 확률은 표본공간에서 다양한 사건이 일어날 가능성을 따지는 것이다. 그러나 때에 따라서는 특정한 사건을 고정하고 그 사건이 일어났다는 조건 하에서 다른 사건이 일어날 확률을 따지는 것이 필요하다. 조건부확률은 이러한 확률을 다루는 개념이다
공식
표본공간 $S$에서 두 사건 $A$와 $B$ 를 생각하자. $P(B)>0$일 때, 사건 $B$가 일어난 조건 하에서 사건 $A$가 일어날 조건부확률은 다음과 같이 정의한다
\[P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{P(A \cap B |S)}{P(B|S)}\]조건부 확률과 독립사건
| $P(B)>0$ 일 때 두 사건 $A$, $B$에 대해 $P(A | B)=P(A)$가 성립하면, 즉 $B$를 조건으로 한 $A$의 확률이나, 그냥 $A$의 확률이 같을 때, 두 사건이 독립이라고 함 |
두 사건 $A$, $B$가 독립이면
\[\frac{P(A \cap B)}{P(B)} = P(A) \Longleftrightarrow P(A \cap B) = P(A)P(B)\]가 성립하므로, 어떤 저자들은
\[P(A \cap B) = P(A)P(B)\]일 때, 두 사건을 독립이라고 정의함
배반사건
같이 일어날 수 없는 사건들을 배반사건이라고 한다. 다시 말해서 표본공간이 $S$인 시행에서 사건, $A$, $B$에 대하여 $A$와 $B$의 곱사건이 공사건이면 ($A \cap B = \varnothing$) 두 사건 $A$와 $B$는 서로 배반한다고 하고 $A$와 $B$는 배반사건이라고 한다. 배타적 사건 또는 서로소인 사건이라고도 부른다. 사건의 확률을 구할 때는 그 사건을 배반사건으로 쪼개 구하는 것이 유용할 때가 많다
배반사건의 성질
표본공간이 $S$인 시행에서 사건 $A$, $B$에 대하여 $A \cap B = \varnothing$이면 사건 $A$와 $B$는 서로 배반한다고 하고 $A$, $B$는 배반사건이라고도 한다. $A$, $B$가 배반사건이면 다음 관계가 성립한다
\[A \subset B^c, \ \ B \subset A^c\]상호배반
사건의 모임 ${A_1, A_2, …, A_n}$ 또는 사건의 열 ${A_1, A_2, … }$에 대하여 어떤 두 사건도 동시에 일어날 수 없으면 상호배반 또는 ‘상호배타적’이라고 한다. 다시 말해서 $i \not= j$ 일 때, $A_i \cap A_j = \varnothing$이면 사건의 모임 ${A_i, A_2, \dots , A_n}$ 또는 사건의 열 ${}$${A_1, A_2, \dots }$은 상호배반이라고 함
상호배반인 사건의 확률
두 사건 $A$, $B$가 상호배반이면 다음 식이 성립한다
\[P(A \cup B) = P(A) + P(B)\]이 결과를 확률의 덧셈법칙이라고 한다. 확률의 덧셈법칙은 n개의 집합에 대하여 다음과 같이 확장할 수 있다. 사건의 모임 $A_1, A_2, \dots, A_n$이 상호배반이면 다음 식이 성립한다
\[P(\cup^n_{k=1}A_k)= \sum^n_{k=1}P(A_k)\]공리적 확률의 정의에 의하면 상호배반인 사건의 열 $A_1, A_2, \dots$에 대하여 다음 식이 성립한다
\[P(\cup^{\infin}_{k=1}A_k)= \sum^{\infin}_{k=1}P(A_k)\]이 식을 확률의 가산가법성이라고 함
전확률(Total Probability)
사건 $A$가 일어날 확률을 여러 배반사건으로 나눠 전체 배반사건의 확률의 합이 사건 $A$의 확률과 같음을 나타냄
→ 전확률은 배반사건의 합
\[P(A)=P(A_1)+P(A_2)+ \cdots +P(A_n)\]- 배반사건의 집합들은 사건 $A$의 부분 집합!
$P(A\ \ A_i)$ (Priori Probability) : 특정 사건($A_i$)이 발생했을 때 전체 사건($A$)이 발생할 확률 - 선행적으로 알고있는 확률
Bayesian Theorem
\[P(B|A) = \frac{P(B \cap A)}{P(A)}\] \[P(A|B) = \frac{P(A \cap B)}{P(B)}\] \[\implies \frac{P(A|B)P(B)}{P(A)}\]$P(A B)$: Priori Probability - $P(B)$:
- $P(A)$: Total Probability로 구할 수 있음
간단히 다음처럼 사용한다
\[P(A_i|A) = \frac{P(A|A_i)P(A_i)}{P(A)}\]- $A$ : 관측된 데이터(Observation Data)/Output
- $A_i$ : Unknown input/original
→ A라는 관측 데이터의 결과(Output)가 $A_i$으로부터 오게 된 것인지 아닌지 가능성을 계산해보는 것!
예시1) Binary Symmetric Channel
Input symbols : ${x_1, x_2}$ → Transmitter
Output(Observation) symbols : ${y_1, y_2}$ → Receiver
→ 입력1을 넣었을때 무조건 출력1이 나올 수 없다. 노이즈가 끼면 신호는 다르게 출력할 수 있기 때문이다
실험적으로 구할 수 있는 요소 → 사전에 알수 있음! Priori Probability
| $P_{11}=P(y_1 | x_1)$ : $x_1$입력일 때 $y_1$ 출력일 확률 |
| $P_{22} = P(y_2 | x_2)$ : $x_2$입력일 때 $y_2$출력일 확률 |
| $P_{12} = P(y_2 | x_1)$ : $x_1$입력일 때 $y_2$출력일 확률 |
| $P_{21} = P(y_1 | x_2)$ : $x_2$입력일 때 $y_1$ 출력일 확률 |
$P(x_1)$ : $x_1$ 입력일 때 확률
$P(x_2):$ $x_2$ 입력일 때 확률
발생할 수 있는 오류 확률 - Unconditioned Error
어떠한 조건없이 무조건 에러가 발생하는 전체확률
\[P_{error} = \text{Prob}(x_1 \ \text{trans},\ y_2 \ \text{receive}) + \text{Prob}(x_2 \ \text{trans},\ y_1 \ \text{receive})\] \[= P(y_2|x_1)P(x_1) + P(y_1|x_2)P(x_2)\]예시2) When $y_2$ received, what probability of $x_1$ transmission?
\[P(x_1|y_2) = \frac{P(y_2|x_1)P(x_1)}{P(y_2)}\] \[= \frac{P(y_2|x_1)P(x_1)}{P(y_2|x_1)P(x_1)+P(y_2|x_2)P(x_2)}\]예시3) $P(x_1|error)$
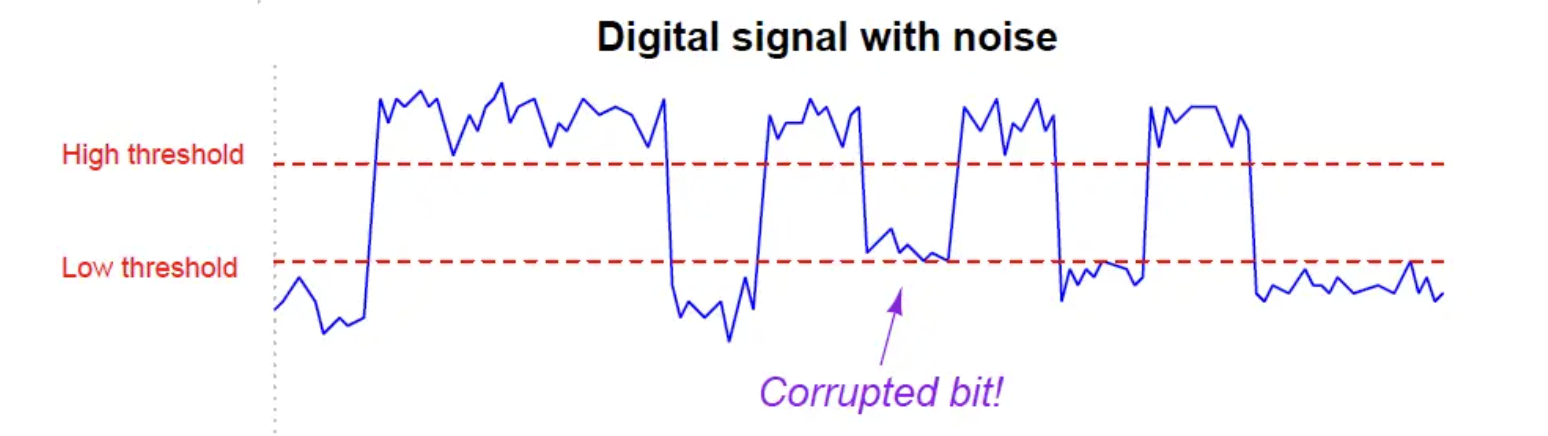
노이즈가 커서 Low값이어야 하는데 High값으로 될 수 있다
Independent Events
$A$ and $B$ are (mutually) independent : 서로 영향을 주지 않음
조건
\[P(B|A)=P(B)\] \[P(A|B)=P(A)\]위 조건 변형하면
\[P(B|A)=P(B)=\frac{P(A \cap B)}{P(A)}\] \[P(A \cap B)=P(A)P(B)\]따라서 다음 조건만 확인하면 독립인지 아닌지 확인 가능
\[P(A \cap B)=P(A)P(B)\]용어 주의 : Independent(독립) $\not=$ Exclusive(배반)
- Independent : 서로 영향을 주지 않음
- Exclusive : 서로 공통된 요소가 없음. 교집합이 없음
- 단, 교집합이 없다고해서 서로 영향을 주지 않는다는 것은 아니다
If A and B are independent:
다음 세 가지 모두 independent
\[A, \ \bar{B} : 독립\] \[\bar{A}, \ B : 독립\] \[\bar{A}, \ \bar{B} : 독립\]- bar 의미 : 여사건
증명
Combined Experiments
For two experiments(동전던지기) with 표본공간 $S_1$, 표본공간 $S_2$,
\[S=S_1 \times S_2\] \[= \{(x_i, y_i)|x_i \isin S_1, \ y_j \isin S_2\}\]- $\times$ : Cartesian Product (순서쌍)
예시) 동전 3개 던지기
$\implies \text{3 experiments of 코인 1개 던지기}$
\[\begin{rcases} S1={H, T} \\S2={H, T} \\S3={H, T}\end{rcases} \implies S=S_1 \times S_2 \times S_3\] \[S = \{HHH, \ HHT, \ \dots \ , \ TTT\} = 8개\]